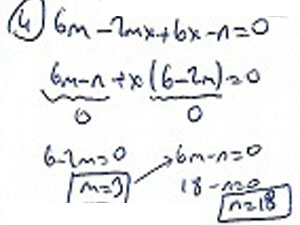2020-2021 9. Matematik Ders Kitabı Cevapları (MEB Yayınları) Sayfa 128 cevaplarını ridkes.blogspot.com aracılığıyla kolayca temin edebilirsiniz. 2020-2021 9. Matematik Ders Kitabı Cevapları (MEB Yayınları) aynı şekilde çözümünü bulamadığınız etkinliklerin çözüm yollarını bu sayfamızdan takip edebilirsiniz. 2020-2021 9. Matematik Ders Kitabı Cevapları (MEB Yayınları) Sayfa 101,102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136,137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188,189, 190, 191, 192, 193, 194, 195 ve diğer Ders kitabı sayfalarına ve diğer birçok kitabın etkinlik çözümlerine sayfamızdan göz atabilirsiniz.
ALIŞTIRMALAR
1. Aşağıda verilen ifadeleri mutlak değer dışına çıkarınız.
a) x ∈ R ve x > 0 ise |5x + 7|
b) x ∈ R ve x < 0 ise |3a - |- a||
c) a, b ∈ R ve 0 < a < b ise |a - b| - |b - a|
ç) x, y ∈ R ve x < y < 0 ise |x + y| + |- x| - |y|
a) x ∈ R ve x > 0 ise |5x + 7| dışarı 5x+7 olarak çıkar çünkü x zaten pozitif bir sayıdır dolayısıyla 5x+7 de pozitiftir dışarı aynı şekilde çıkar.
b) x ∈ R ve x < 0 ise |3x - |- x||
I-xI dışarıya -x olarak çıkar çünkü x negatif bir sayıdır önüne - işareti gelince pozitif olur. I3x-(-x) I=I4xI oldu, I4xI dışarıya pozitif olması için -4x olarak çıkar
c) a, b ∈ R ve 0 < a < b ise |a - b| - |b - a|
(a-b) negatif bir sayıdır çünkü b a dan büyüktür.Bu yüzden Ia-bI dışarıya önüne - alarak b-a olarak çıkar.
(b-a) pozitif bir sayıdır çünkü b a dan büyüktür.Bu yüzden Ib-aI dışarıya pozitif olduğu için aynı şekilde çıkar b-a olur.
(b-a)-(b-a)=0 olur.
d) x, y ∈ R ve x < y < 0 ise |x + y| + |- x| - |y|
Ix+yI ifadesi x ve y negatif olduğu için negatif bir sayıdır ve mutlak değer dışına önüne - alarak çıkar -x-y olur
x negatif bir sayı olduğu için -x pozitif bir sayıdır bu yüzden I-xI ifadesi dışarıya aynı şekilde -x olarak çıkar
y negatif bir sayıdır bu yüzden IyI dışarıya önüne - alarak çıkar -y olur
-x-y-x-(-y)=-2x oldu
2. Aşağıda verilen mutlak değerli denklemlerin çözüm kümelerini bulunuz.
a) x ∈ R , |- 2x + 7| = 11
b) x ∈ R , |- 7x + 17| = -2
c) a ∈ R , |5a - 20| = 0
ç) b ∈ R , |- 3b| + |2b| - 20 = 0
a) Mutlak değerin içini önce 11'e daha sonra da -11'e eşitleyerek işlem yapacağız. Mutlak değer bütün sayıları pozitif yaptığından dolayı içindeki sayıların negatif olma ihtimalini de düşünmüş oluyoruz böylece.
-2x + 7 = 11
-2x = 4
x = -2
-2x + 7 = -11
-2x = -18
x =9
Bu işlemlerden anlarız ki x'in -2 ve 9 olmak üzere iki değeri olabilir.
b) Mutlak değerin eşit olduğu sayı hiçbir zaman negatif olamayacağı için x yerine hangi sayıyı yazarsak yazalım bu ifade sağlanamaz. Yani x değerini sağlayan elemanlar kümesi aslında bir boş kümedir.
c) Mutlak değerin içindeki sayı 0 ise eşit olduğu sayı da 0 olur. O halde;
5a - 20 = 0
5a = 20
a = 4 olmalıdır.
ç) Bu soruyu çözerken iki ihtimal için işlem yapmalıyız. b sayısı negatif veya pozitif olabilir. Her ikisini de değerlendirmeliyiz.
* b < 0
-3b -2b = 20
-5b = 20
b = -4
* b > 0
3b + 2b = 20
5b = 20
b = 4
Yaani b sayısı -4 veya +4 olabilir.
3. Aşağıda verilen mutlak değerli eşitsizliklerin çözüm kümelerini bulunuz.
a) x ∈ R , |5x - 5|< 10
b) a ∈ R , |7a - 13| < 0
c) a ∈ R , |6a - 12| < -7
ç) a ∈ R , |2a - 2| - 8 ≤ 0
d) x ∈ R , |x + 6| > 0
e) x ∈ R , 6 ≤ |x - 8| ≤ 10
a) |5x - 5| = 10
Mutlak değerin içinin negatif veya pozitif olmasına göre işlemi iki kere yapacağız.
* -5x + 5 =10
-5x = 15
x = -3
* 5x - 5 =10
5x = 15
x = 3
Bu sayılar mutlak değerin içini 0 yapan sayılardır. Yerine yazdığımızda 10'dan küçük gelmesi gerektiği için x çözüm kümesi (-3 , +3) olarak bulunur.
b) Bu ifade mutlak değerin sonucunun 0'dan küçük olmasını istiyor bizden. Ancak mutlak değer sonucu her zaman pozitif olduğu için bu ifade yanlıştır. x yerine yazılabilecek bir sayı yoktur. x kökleri boş kümeyi ifade eder diyebiliriz.
c) | x + 6| > 0
Mutlak değerin sonucu her zaman pozitiftir. Mutlak değer içini 0 yapan değer hariç tüm sayılar x değeri olabilir. Yani x "-6" hariç tüm sayılardır.
ç) Bu seçeneği değerlendirirken mutlak değer içindeki sayının negatif olması ihtimalini de düşüneceğiz. Şöyle düşünebiliriz; (x-8) sayısı mutlak değer içinde olduğu için dışarıya daima pozitif çıkacaktır. x yerine yazdığımız değer sonucu bu sayı 6 da olabilir -6 da olabilir ancak sonuç her zaman 6 olmalıdır.
* 6 ≤ x-8 ≤ 10
14 ≤ x ≤ 18
Bu işlemlerden x sayısı 14, 15, 16, 17 ve 18 çıkar.
* -6 ≥ x-8 ≥ -10
2 ≥ x ≥ -2
Bu işlemlerden de x sayısı 2, 1 , 0, -1 ve -2 olarak bulunur.
x yerine 10 tane sayı yazılabilir ve bu sayılar {-2,-1,0,1,2,14,15,16,17,18}'dir.
4. x ∈ R olmak üzere ||x - 4| - 6| = 2 denkleminin çözüm kümesini bulunuz.
5. x, y ∈ R olmak üzere |x - 3| < 5 ve 3x - y = 2 ise y nin alabileceği kaç farklı tam sayı değeri olduğunu bulunuz.
6. Sayı doğrusu üzerinde 7 ye olan uzaklığı 5 birimden fazla olmayan kaç tane tam sayı değerinin olduğunu bulunuz.
Bir sayı doğrusu üzerine tam sayıları yazdığımızı düşünelim. 7 noktasına olan uzaklığı 5 birimden fazla olmayan tam sayıları yani en fazla 5 birim olan sayıları tek tek işaretleyelim.
7-5 = 2
Sayı doğrusunda 7'ye 5 birim uzaklığındaki en küçük sayı 2'dir.
7+5 = 12
Sayı doğrusunda 7'ye 5 birim uzaklığındaki en büyük sayı 12'dir.
Soruda bizden istenen sayılar 2 ile 12 arasında kalan sayılardır. 2 ve 12 de bu sayılara dahildir.
2, 3, 4, 5, 6, 8, 9, 10, 11, 12
Toplam 10 tane sayı vardır.
7. 2/|a - 2| > 1/3 eşitsizliğini sağlayan kaç farklı a tam sayısının olduğunu bulunuz (a nın 2 olamayacağına dikkat ediniz.).
Öncelikle her iki sayının da pay kısmını eşitleriz. Böylece paydalar arasında kıyaslama yapabiliriz.
Paydaya 2 değerini de yazamayacağımız için özellikle dikkat etmeliyiz. İşlemleri ekte bulabilirsin.
2 / (1a - 21) > 1 / 3
2 / (1a - 21) > 2 / 6
6 > 1a - 21
6 > a - 2 > -21
a = {7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3}